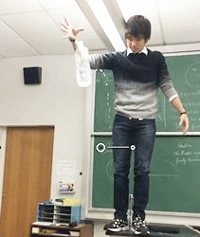１．自由落下、投げ上げ、斜方投射 （放物運動）
１）Fig.16のようにペットボトルにストローを接着剤で取り付け、ボトルに水を入れてふたを取り外したものを用意する（A）。これを自由落下などの運動をさせて水流の変化を観察する（B).
２）自由落下： 実験のビデオ（Fig.17a）とアニメ（Fig.18)が示すように落下時に水流は止まる。
３） 投げ上げ：アニメ（Fig.19）が示すように運動中に水流は止まる。
４）斜方投射：ビデオ（Fig.17b）では上昇中に水流は止まっているが最上部で回転が起こったためか水が落ちている。アニメはFig.20。
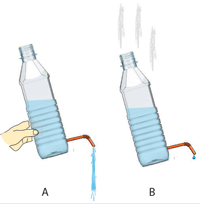
Fig.16 ストローをつけたペットボトル
手に持つと水が出るが自由落下させると止まる
Fig.17a ペットボトルの自由落下
Fig.17b ペットボトルの斜方投射
3 
Fig.18 自由落下
Fig.19 投げ上げ
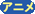Fig.20 斜方投射
Fig.20で示した斜方投射と同様な運動を航空機で行う「無重力状態」が実用化されている(Fig.21)。航空機の運動はFig.22のアニメでに示したように、ジェットエンジンで上昇後エンジンの駆動を止めた状態で放物運動をする。このとき、およそ１５秒程度の「無重力状態」が生じる。
Fig.22 航空機による「無重力状態」の実現
（ひげじい）「ちょっと待った！ エレベーターが宇宙で自由落下するときに中にいる人が「無重力」のようにフワフワするのは自由落下と落体の法則で説明できるとわかったけど、ペットボトルが投げ上げられたり、飛行機が上昇しているときには、落下していないわけだから「自由落下」で「無重力状態」を説明するのは無理があると思うけど？」３．慣性運動
投げ上げや斜方投射などのような放物運動 projectile motion で単純な自由落下 free fall と同様な「無重力状態」がなぜ現れるか、を説明するには、慣性 inertia の理解が必要であろう。
１６世紀まで、馬車を動かすには馬が絶えず引く力が必要なことから、「物が運動を続けるには力が必要不可欠である」とされた(Fig. 23)。しかし、この考え方では、弓から放たれた矢には力が働いていないように見えるのになぜ飛び続けるのかがうまく説明できなかった(Fig. 24)。ガリレオは、転がる球の観察から、「動いている物体は、力がはたらかなくても動き続ける性質がある」と結論してその性質を「慣性 inertia」と呼んだ。ニュートンは、慣性による運動を第一法則、力による運動を第二法則として運動の基本法則とした。
Fig.23 馬車
Fig.24 飛ぶ矢エアトラック
Fig. 25のアニメで示されるエアトラックは、屋根型の面に多数の小さな穴が開けられ、ここから吹き出す空気がカートと屋根型レールの摩擦を小さくしている。こうして、カートは屋根型レール上を滑らかに動くことができる。
アニメのように、カートを動かして初速度を与えると長時間 動く様子が観察できる。レールの端にある、ぴんと張ったゴム紐に衝突すると向きを変えて、速さはほとんど変化せず運動を続ける。
一方向に進行中のカートに働く力は下向きの重力と吹き出す空気による上向きの垂直抗力で、二つの力は釣り合っている。カートの進行方向の力は（進行の向きとは逆向きの）摩擦力であるが、吹き出す空気の作用により摩擦は小さく無視できるとしてよい。したがって、カートにはたらく力の和（合力）はゼロ。カートが運動を続けるのは慣性によるもので「慣性運動」である。
ゴム紐との衝突では、カートがゴム紐を押す結果、ゴム紐がカートを押し返す力が働く（作用反作用の法則）。衝突は「弾性的」でカートの運動エネルギーは保存されるので、進行方向は逆向きになるが速さは衝突前と同じである。「慣性運動」は継続する。
Fig.25 
エアトラック
・信号が多かったり路面に抵抗の多い近道より、遠回りでも自動車専用道路の方が慣性走行ができるので経済的かも。
Fig. 26 生徒実験
ボール落下/打ち上げカート
ボール落下/打ち上げカート
(Pasco社製Ballistic cart)
カート上の柱の頂上に金属を内包するプラスチック球が電磁石で仮固定されている。レール上に、この電磁石のはたらきを切断するスイッチがある。初速度を与えられて慣性運動しているカートがこのスイッチを通過した瞬間にボールが落下する。
レールに対して静止している観察者Aは、磁石を離れたボールが「水平投射」の運動をすると理解する。一方、カートに乗った観察者Bは、ボールが単純な「自由落下」運動をすると理解する（Trajectoryを参照しよう）。これは、高速で等速直線運動する新幹線車内で ボールを落としたとき単純な自由落下となることからも理解されよう。
Fig.27 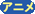ボール落下カート
マウスを上の図上に置くとアニメ、右手のTrajectory上に置くとボールとカートの軌跡が 観察できる。
４．運動の解析（１）
自由落下（A）、投げ上げ（B）、水平投射（C）、斜方投射（D）の４っつの運動を「慣性」と「自由落下」の立場で解析してみよう。まず、Fig.27のボール落下カートにおけるボールの運動の、観察者Aから見た軌跡がFig. 28の(C)である。ボールは、水平方向に等速度
で運動する「慣性運動」と鉛直下向きに加速度
で運動する「自由落下」をベクトル的に足し合わした運動ととらえることができる。同時に、ボール落下カートの実験からわかるように、慣性運動と共に動く系（慣性座標系）では自由落下運動のみの運動としてとらえて良い。
（B)投げ上げ運動でも同様の解釈が可能であり、鉛直上向きに 等速度で運動する「慣性運動」と鉛直下向きに加速度で運動する「自由落下」がベクトル的に足し合わされた運動をすると見なされる。慣性運動は質量に寄らないからボトルと水は同一の運動をする。投げ上げられたペットボトルと水の場合でも慣性運動は両者の位置関係に関係しないと見なすことができ、両者は自由落下運動状態にあり水流が止まり、「無重力状態」となることが理解できる。
（D）斜方投射でも同様で、 水平方向に
鉛直上向きに
の速度をもつ慣性運動の系では物体は自由落下運動をしている。ペットボトルの斜方投射での「無重力状態」もこうして理解されよう。
ただし、ペットボトルの斜方投射の実験結果で見られたように、物体が回転運動をした場合には「無重力状態」とならない場合がある。この点はあらためて考察しよう。
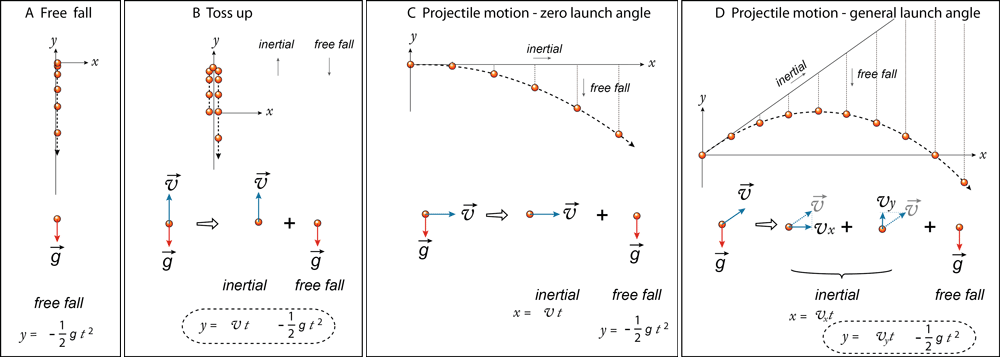
Fig.28 運動の解析（１） 投げ上げ（B)、水平投射（C)、斜方投射（D)などの運動は、慣性運動(inertial)と自由落下(free fall)をベクトル的に足し合わせた運動である。
４．運動の解析（２）
上の運動の解析（１）では、放物運動が運動全体として慣性運動と自由落下を足し合わせたものとして解析した。別の見方として、斜方投射を例として運動している物体の一瞬一瞬を考えよう。
Fig.29は、投げ上げられてから一定時間ごとの（つまり一定水平距離pごとの）物体を示している。n−１番目の物体はその時の運動の接線方向にその時の速さで慣性運動(inertial)すると同時に重力による落下運動をすると見なすことができる。こうしてn番目の物体の位置と速度は、直前n−１番目の慣性運動と自由落下を足し合わせたものになる。こうした運動が連続して起こるものと解釈できる。
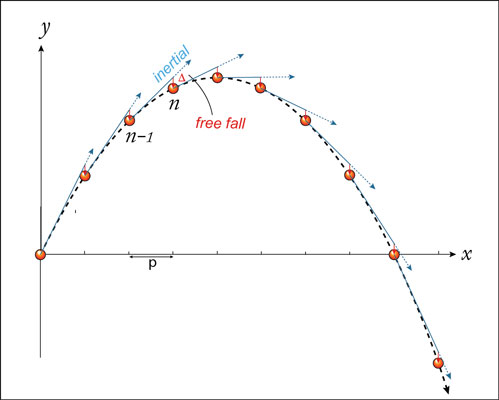
Fig.29 運動の解析（２） 斜方投射（D)は慣性運動(inertial)と自由落下(free fall)を足し合わせた運動が連続していると見ることもできる。
６．結論
物体を放り投げる運動は、どれも慣性運動と自由落下という２つの運動を（ベクトル的に）足し合わせた運動となる。慣性運動も自由落下運動も質量に寄らず同一であるから落体の法則が成立する。容器とその中の物体を放り投げたときは両者が同一の運動、つまり慣性運動と自由落下を足し合わせた運動、となり、中の物体は容器から力を受けることがなく「無重力状態」となる。ただし、物体が回転運動などを起こした場合には無重力状態とならない場合がある。