D-3では、投げ上げや斜方投射のような地上から上方に向かっている運動中にも「無重力状態」が起きていることを実験などで示し、これを「慣性運動」と「自由落下」の2つの運動の合成として解釈し「無重力状態」を説明した。
本節では軌道運動を解析して「無重力状態」のメカニズムを考えよう。
1.軌道運動
ロケットを水平方向に発射する。推進のための力は発射の瞬間だけはたらき、その後にロケットにはたらく力は重力だけとする。初期速度![]() が比較的小さい場合(Fig.30)は、放物線軌道で地上に落下する。初期速度が大きくなると(Fig.31)、ロケットにはたらく重力は地球の中心を向くので楕円軌道としてとらえる必要がある。
が比較的小さい場合(Fig.30)は、放物線軌道で地上に落下する。初期速度が大きくなると(Fig.31)、ロケットにはたらく重力は地球の中心を向くので楕円軌道としてとらえる必要がある。
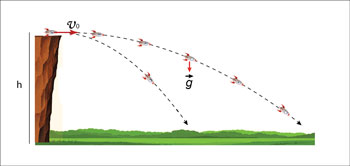
Fig.30 水平投射-1 地上h[m]から初速度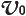 [m/s]で水平方向に発射されたロケットには鉛直下向きに重力がはたらき,放物線を描いて地上に落下する。
[m/s]で水平方向に発射されたロケットには鉛直下向きに重力がはたらき,放物線を描いて地上に落下する。
Fig.31で、ロケットを発射する高さと発射速度は以下のように設定している。
高さ h:784 km
発射速度 ![]() 軌道1:2.36 km/s
軌道1:2.36 km/s
軌道2:4.72 km/s
軌道3:6.24 km/s
軌道4:7.08 km/s
軌道5:7.27 km/s
軌道6:7.46 km/s
軌道7:8.18 km/s
軌道8:9.14 km/s
計算に用いた諸量
万有引力定数 G: 6.67430 x 10-11 N・m2/kg-2
地球の平均半径 RE: 6.371 x 106 m
地球の質量 ME: 5.972 x 1024 kg
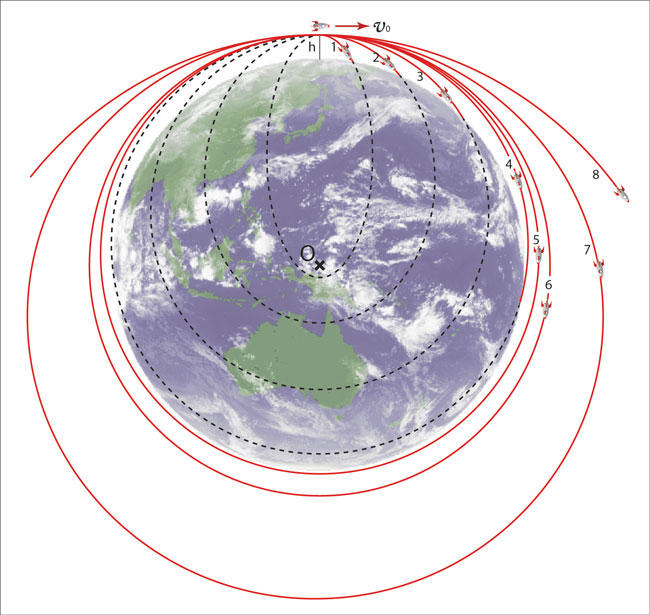
Fig.31 水平投射-2 より高速の初速度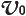 [m/s]で水平方向に発射されたロケットの軌道。ロケットにはたらく重力の向きは地球の中心方向で、楕円軌道を描いて地上に落下する(軌道1〜4)。初速度がさらに大きくなると、地上に落下せず周回する(軌道5〜8)。軌道6は、地上から軌道までの距離が常に等しい「円軌道」。
[m/s]で水平方向に発射されたロケットの軌道。ロケットにはたらく重力の向きは地球の中心方向で、楕円軌道を描いて地上に落下する(軌道1〜4)。初速度がさらに大きくなると、地上に落下せず周回する(軌道5〜8)。軌道6は、地上から軌道までの距離が常に等しい「円軌道」。
2.軌道運動の運動方程式による解析
宇宙船内で乗組員がフワフワと「無重力状態」になることは、高校物理では次のような計算で理解される。

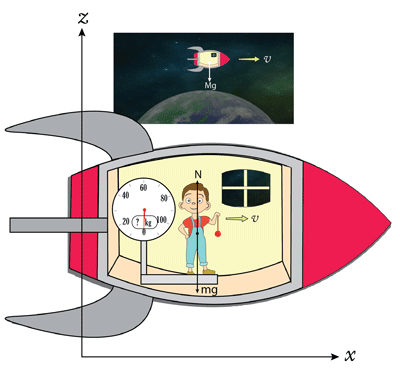
Fig.32 地球を周回する宇宙船、宇宙船内の体重計に乗る少年
この高校物理の解法で、少年が「無重力状態」となるのは問題なく説明されている。ニュートンの運動方程式と作用反作用の法則を正しく使えば多くの力学の問題がスラスラと解ける。それでも、式では解けたけれども「結局無重力状態になる理由は何だろう?」という疑問が湧く。このあたりが、物理が難しく、また面白いところである。
また、楕円軌道などを運動方程式で解くのは容易ではない。
3.軌道運動の図による解析
「なぜ宇宙船内で無重力状態になるか」という理由を知るために、前節で自由落下、放物運動で採用した図を用いた方法を軌道運動にも応用してみよう。軌道運動は通常採用される円運動とし、前節の放物運動における運動の解析(2)と同様な解析をする。円運動をする宇宙船(および乗組員)は常時接線方向に慣性がはたらく。慣性運動をFig.33-Aで青色で示した。宇宙船(および乗組員)には慣性に加えて常時地球の中心方向に重力が働く。重力による自由落下運動をFig.33-Aで赤色で示した。つまり、慣性運動で地球から遠ざかった分だけ自由落下で地球に引き戻されて、その二つの運動が釣り合って円運動になるというわけだ。回転角θごとに運動が合成されるとしている。θを限りなく小さくすれば二つの運動の合成が連続的に起こると言える。
慣性運動は質量に無関係に全く同じ挙動をするので運動中に宇宙船と乗務員の相対関係は 変わらない。宇宙船も乗務員も慣性運動しながら絶えず自由落下運動をしている。その結果奇妙なことであるが、地球からの高度は一定のまま自由落下運動を続けている。表現を変えると、軌道運動では進行方向に直線上に進んで軌道から外れるような慣性がはたらくが、重力の自由落下運動で軌道上に引き戻しているわけだ。これが、宇宙船内で乗務員がフワフワと「無重力状態」となる理由である。
![]() (ひげじい)「ちょっと待った! 自由落下運動をする赤い宇宙船が何もないところから落ちてくるのがおかしい!
(ひげじい)「ちょっと待った! 自由落下運動をする赤い宇宙船が何もないところから落ちてくるのがおかしい!
上の図を描き直したのがFig.33-B。軌道運動を、軌道の接線方向の慣性運動と地球に向く自由落下運動に分けている。軌道運動は二つの運動が(ベクトル的に)合成されたものとみなすことができる。
Fig.33-A 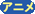 宇宙ステーションISSの軌道運動を、接線方向の「慣性運動」と地球の中心方向の「自由落下」の2種類の運動の組み合わせととらえている。
宇宙ステーションISSの軌道運動を、接線方向の「慣性運動」と地球の中心方向の「自由落下」の2種類の運動の組み合わせととらえている。
Fig.33-B 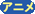 宇宙ステーションISSの軌道運動の解析 軌道の円運動を、接線方向の「慣性運動」と地球の中心方向の「自由落下」の2種類の運動の合成ととらえている。
宇宙ステーションISSの軌道運動の解析 軌道の円運動を、接線方向の「慣性運動」と地球の中心方向の「自由落下」の2種類の運動の合成ととらえている。
4.円軌道以外の運動をする宇宙船
楕円軌道 地球を周遊する宇宙船は円に近い軌道とする場合が多いが、それは地表との距離が変わらない方が通信などの点で便利だからであろう。より一般的な軌道としては、地表との距離や速さが絶えず変化する楕円軌道をとることもできる(Fig.31)。楕円軌道の場合にも「無重力状態」となるだろうか?楕円運動でも「無重力状態」となる事情に変わりがない。これは、Fig.33-Bで、慣性運動の速さが違うだけで楕円運動となることから容易に理解できる。これが図による軌道解析の利点である。楕円運動の運動方程式を検討するよりずっと易しい。
宇宙旅行 また、アポロ宇宙船などの例のように、月や惑星に向かう「宇宙旅行」でも大部分の時間はジェット噴射などの推進力を使わない「慣性飛行」をする。その旅行中は、出発時の速度で決まる「慣性運動」と、衛星、惑星、太陽の重力(の合力)による「自由落下運動」が合成された運動をしているので、同様な理由で「無重力状態」での旅行となる。

5.「月は地球に向かって落ち続けている」 - ニュートン
宇宙船の話からそれるが、月も地球に向かって落ちていることについて話そう。
西暦1666年ごろ、ニュートンは自身が見出した運動の3法則は地上で起こる物理現象だけでなく天体にも応用できるのではないかと考えた。特に、惑星の軌道運動についてのケプラーの3法則に適用した結果、2個の天体(1と2)の間に次の力(万有引力)がはたらくことを見出した。
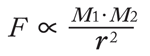 (r は天体1と天体2の間の距離)
(r は天体1と天体2の間の距離)
さて、こうして導かれた万有引力F は地上ではたらく重力と同じものだろうか?この問いの検証として地球を周回する月を選んだが、当時、地球、他の惑星、月などの質量はどれも知られていなかった。ニュートンは、月もりんごと同様に地球に向かって落下しているに違いないと考え、その落下の速さを検討した。
右の図で、月は軌道の接線方向に1秒間にx [m]進んでいる間にs [m]落下して軌道に戻るとした。月の公転周期T は27日((1)式)。地球と月の距離R は日食観察から地球の半径r の60倍と測定されていた。r の測定値を用いて、式(4)からx =1029m 。2個の相似の三角形から式(5)、(6)より、s =0.0014[m]。つまり、月は、1秒間に、およそ1.0km接線方向に進む間に1.4mm地球に向かって落ちることが月の軌道の大きさと周期から導かれる。
一方、地上近くのりんごが1秒間に落下する距離は式(7)で、s' =4.9[m]。もし、りんごが月の軌道にあったら?地球中心-月の距離は地球中心-地表の距離の60倍だから、月の軌道における重力加速度gは「逆二乗則」により1/602になるだろう。式(8)で計算すると、s" =0.0014[m]、1.4mm、となり、式(6)の値と良い一致を示す。(良すぎる一致だが・・・)
地上の運動法則が天体の運動にも適用できることを示唆する画期的な検証となった。

月も、りんごのように落ちているに違いない...
"The Moon is constantly falling towards the Earth, although it never falls down."
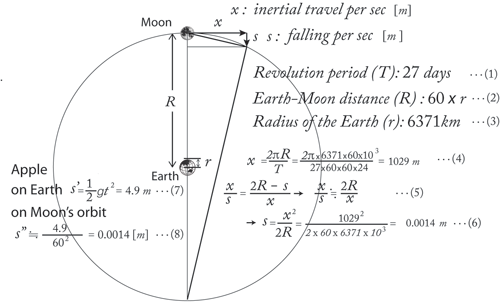
月が地球に向かって落ちる距離とりんごが落ちる距離の比較
6.「完全無重力」、自由落下、軌道運動 (参考)
![]() (ひげじい)ISSの軌道運動は自由落下運動と慣性運動が組み合わさった運動だから「無重力状態」になる、という説明だと理解したけど、「完全な無重力状態」と「自由落下や軌道運動の無重力状態」とは区別がつくの?」
(ひげじい)ISSの軌道運動は自由落下運動と慣性運動が組み合わさった運動だから「無重力状態」になる、という説明だと理解したけど、「完全な無重力状態」と「自由落下や軌道運動の無重力状態」とは区別がつくの?」
太陽系の中では太陽、惑星、衛星などの重力の影響がどの場所でもあり 、太陽系の外でも「完全に重力がない」場所というのは考えずらい。が、仮に、「完全な無重力」の場所があるとしよう。そのような場所と、自由落下や軌道運動における「無重力状態」は次の思考実験で識別できるであろう。
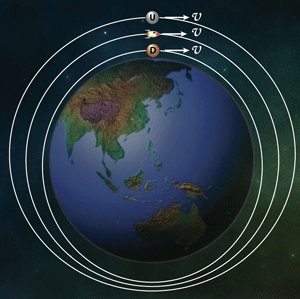
宇宙船内にFig.34のように6個のボールを浮かせて置く。
ボール R、L: 重力の方向に対して垂直、宇宙船の重心の右と左に並んでいる。
ボール F、B: 重力の方向に対して垂直、宇宙船の重心の前後に並んでいる。
ボール U、D: 重力の方向に平行で、Uは宇宙船の重心の上、Dは下。
野球ボール: 宇宙船の重心の位置。
ボールとボールの間の万有引力の影響は無視できるとして、各ボールが時間と共にどのように動くか考えよう。
完全無重力ではもちろん6個ともいつまでもその場所に止まっている(Fig.34)。
![]() 2 宇宙船が地球に向かって自由落下しているとき(Fig.35)。6個のボールはどのように変化するだろうか?
2 宇宙船が地球に向かって自由落下しているとき(Fig.35)。6個のボールはどのように変化するだろうか?
![]() 3 地球の周りを円軌道運動している場合{Fig.36)はどうか?
3 地球の周りを円軌道運動している場合{Fig.36)はどうか?
![]() 4 軌道運動する宇宙船の中で、野球のボールを宇宙船の重心の位置に置いた後、前方に投げる(Fig.37)。あるいは後方に投げる(Fig.38)。ボールはどのように動くだろうか?
4 軌道運動する宇宙船の中で、野球のボールを宇宙船の重心の位置に置いた後、前方に投げる(Fig.37)。あるいは後方に投げる(Fig.38)。ボールはどのように動くだろうか?
(筆者の答えは、図上にマウスを置いたときのアニメ。)
![]() 5 ボールがアニメのように動く理由を説明せよ(ヒントは下記。)
5 ボールがアニメのように動く理由を説明せよ(ヒントは下記。)
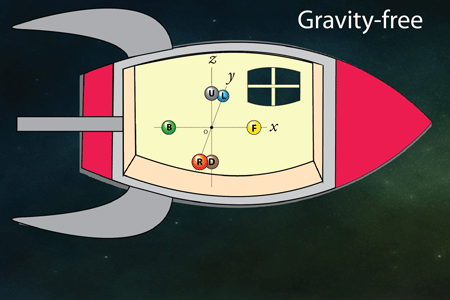
Fig.34 1)完全に無重力 --- ボールは動かない
Fig.35  2)地球に向かって自由落下
2)地球に向かって自由落下
Fig.36 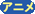 3) 地球の周りを円軌道運動
3) 地球の周りを円軌道運動
Fig.37 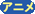 4)円軌道運動 ボールを前方に投げる
4)円軌道運動 ボールを前方に投げる
Fig.38 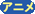 5)円軌道運動 ボールを後方に投げる
5)円軌道運動 ボールを後方に投げる
クイズ5のヒント
2)地球に向かって自由落下 地球の中心に向かって落下していくので、 R、L、F、Bは宇宙船の重心に集まるように動く。これは潮汐効果の一つである(Fig.39 )。
重力の大きさは、宇宙船の重心の上側、重心、下側の順に強くなる。潮汐効果(Fig.39 )。
3)地球の周りを円軌道運動 R、Lは重心の円軌道に対して傾いた円軌道上を運動する(Fig.40)。R、L、重心の3個の軌道は1/4周期回ったところで出会い、R、Lはその時衝突する(Fig.31の円軌道では周期は100分なので出会うのは25分後。) F、Bは重心と同じ軌道上だからこのこの効果はないが、潮汐効果で重心に向かって動くとも考えられる(アニメ)がその効果は小さいであろう。
U、Dは、(地球に向かって自由落下と同様に)潮汐効果で宇宙船の重心から離れるように動く、という説明がある。4また、両方ともおかしな動きをする、との説明もある。3 私は、Fig.31の軌道でスタート時の高度を変化させた場合の図、Fig.41を基に考察するとアニメのように動くと考える。つまり、宇宙船の軌道の外側にあるUは円軌道に必要な速度より小さい速度なので最初は宇宙船に遅れてかつ地球に接近する。またDはその逆で、宇宙船より先行しかつ地球から離れる。
4)円軌道で運行する宇宙船(あるいは物体)を加速すると、円軌道より外側の楕円軌道となり周期は長くなる。遅い宇宙船(あるいは物体)は逆で内側の楕円軌道となり周期は短くなる。(Fig.31) 1周期ごとにほぼ元の位置に戻り、それぞれ元の位置の後方または前方に戻る。3
7.結び
以上が「宇宙船の中で乗組員がフワフワ無重力状態になるのはなぜか?」という問題についての考察です。
これを読んでいただいて何かお役に立てたら嬉しいです。 ご意見を歓迎します。
6.文献
1.Wikipedia, "Weightlessness"
2. Britannica, "Weightlessness"
3.D. Chandler, "Weightlessness and microgravity," Phys. Teach. 29 312 (1991).
4.I. Galili and Y. Lehavi, "The importance of weightlessness and tides in teaching gravitation," Am. J. Phys. 71 1127 (2003).
5.P. Mohazzabi, Phys. Teach. 44 240 (2006).
6.A. A. Bartlett, ""Apparent Weight": A Concept that Is Confusing and Unnecessary," Phys. Teach. 48 522 (2010).
7.W. D. Pesnell, "The flight of Newton's cannonball," Am. J. Phys. 86 338 (2018).
8. P. Hewitt, "Figuring Physics: Nellie's Satellite Speed," Phys. Teach. 56 277 (2018).
9.C. E. Mungan, "Orbital speed of a satellite due to gravity," Phys. Teach. 56 339 (2018).
10.森谷東平, 「静止衛星打ち上げの計算」 (2016).
11.J. Balukovic, J. Slisko and A. C. Cruz, "A Person Stands on a Balance in and Elevator: What Happens When the Elevator Starts to Fall?," Phys. Teach. 56, 156 (2018).
12.A. M. Nobili et al., "On the universality of free fall, the equivalence principle, and the gravitational redshift," Am. J. Phys. 81, 527 (2013).

Fig.39 潮汐効果
白矢印は重力の向きと大きさ。赤矢印は宇宙船の重心の重力と各ボールの重力の差分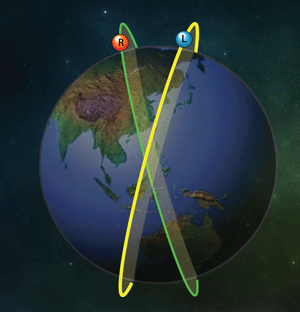
Fig.40 傾きのある2個の円軌道
軌道が2箇所で交わっていて、ここで2個のボールは出会い衝突する。