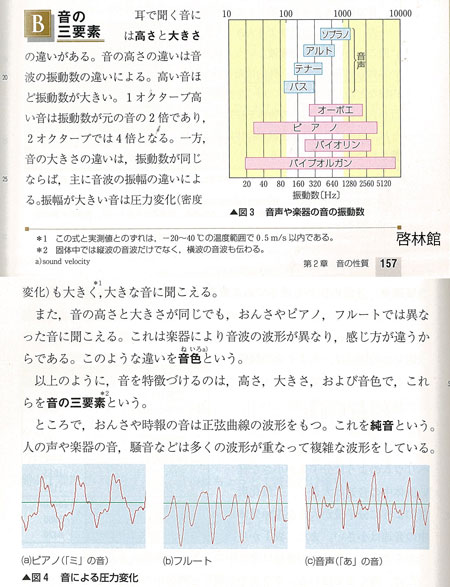
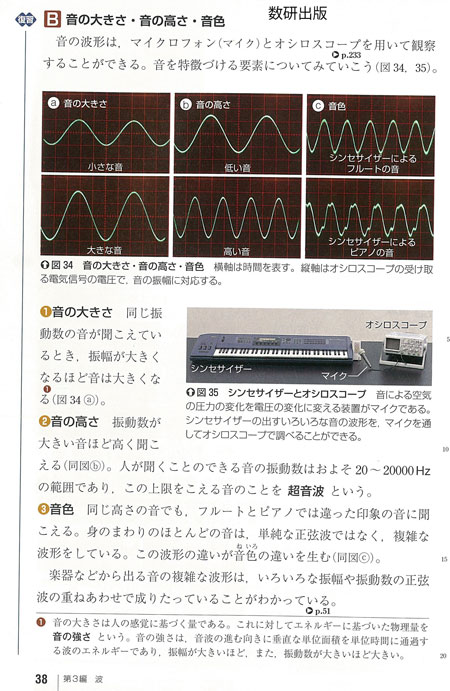
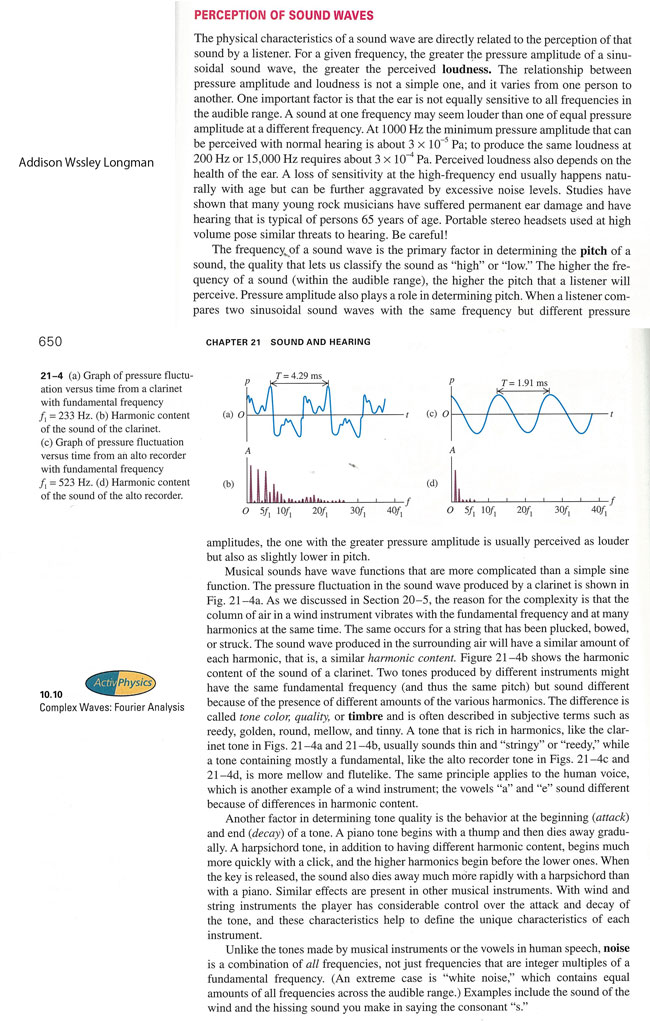
音の高さPitchは、音楽でメロディの元だからとても重要だ。日本の教科書には「音の高さはその振動数で決まる」とありそれ以上の説明がない。しかし、物理を少し学んだら話はそう簡単ではないと気づく。なぜなら、音叉など単一の振動数を持つものはまれで、楽器の音やヒトの声は倍音harmonicと呼ばれる多くの振動数を含むから。楽器は倍音構造が異なるのに合奏で高さを合わせられるのはどうしてだろうか。音の高さはどのようなメカニズムで決まるのだろう?こんな素朴な疑問についての解説がほとんど見当たらないのも不思議だ。倍音を含む音では最も低い振動数である基音fundamentalが音高pitchを決めるという解説もあるが、それはどうしてなのだろう?それに今回実施した楽器や人の声の振動数分析では、基音は必ずしも強度が大きいわけでなく、中には極めて弱い例もあるのに驚かされる。基音の強度がゼロである音も珍しくはないそうでミッシングファンダメンタルmissing fundamentalと呼ばれているが、含まれない振動数が音高を決めるというのも不思議である。
2021.3.20 森谷東平
1)実験と解析
インターフェース:Vernier社LabPro
音波解析ソフトウェア:Vernier社LoggerPro
正弦波の和の波形:Apple Grapher、
PC: MacBook Air
2)楽器と人の声の振動数分析結果
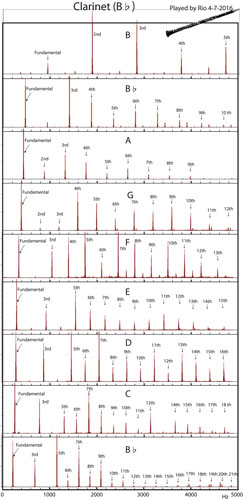
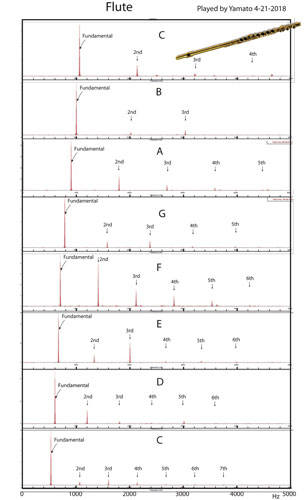 Fig. 1 クラリネット Fig.2 フルート
Fig. 1 クラリネット Fig.2 フルートクラリネット(Fig.1)
・どの音も多くの振動数を含む。・図の 一番下のB♭の音は、最も低い振動数は233Hzでこれが基音 fundamental で、次が699Hz(3倍音)、1166Gz(5倍音)。次に1399Hz(6倍音)の小さいシグナルの後1631Hz(7倍音)、8倍音、9倍音・・・と続いている。強度の高いものは、9倍音までの奇数倍音で、その強度も基音と同じレベルである。6倍音以上では小さい偶数倍音がある。
・B♭と同様な傾向がC、D、Eに見られる。
・Fでは3倍音の次に4倍音が基音と同程度の高いレベルである。また、Gでは3倍音が小さく4倍音が大きい。
・クラリネットの音で奇数倍音が多く含まれることは、この楽器が「片側閉管楽器」としての性格が強いとすればうまく説明できる。
・含まれる振動数の強度を比較すると、強度の大きい倍音がたくさんあり、基音の強度が必ずしも特別大きいわけでもないことに驚かされる。「音高」pitch を決めているのは何か?という疑問が湧く。
フルート(Fig.2)
・全体に見ると、倍音が比較的少なくて純音に近い。クラリネットと対照的である。倍音は偶数倍音、奇数倍音ともにあり、この楽器が「開管楽器」とするモデルに対応している。
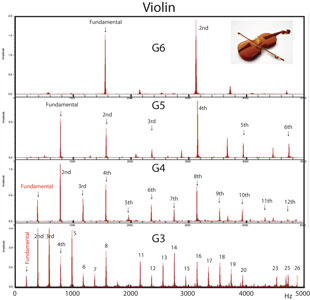
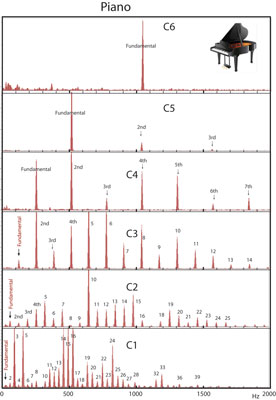 Fig.3 バイオリン
Fig.4 ピアノ
Fig.3 バイオリン
Fig.4 ピアノバイオリン(Fig.3)
・まず驚かされるのは、G3もG4の音も基音の強度が倍音の強度よりも小さいことである。G3の基音は特に弱く、ミッシングファンダメンタルに近い。・低い音では多くの倍音を含むのに比較して高い音では比較的倍音が少ない。
ピアノ(Fig.4)
・低音ほど倍音の数が多い点、基音の強度が極端に小さい音がある点、はバイオリンと同様な傾向である。C1〜C3ではミッシングファンダメンタルに近い。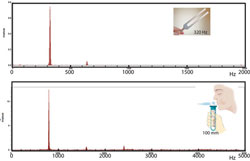 Fig.5(上)おんさ(320Hz)(下)100mm長の試験管
Fig.5(上)おんさ(320Hz)(下)100mm長の試験管 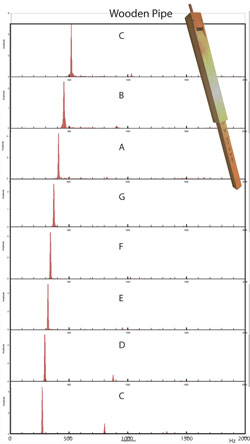 Fig.6 物理実験用の木製管楽器
Fig.6 物理実験用の木製管楽器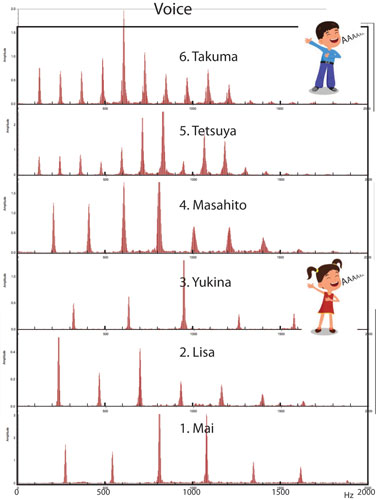
おんさ320 Hz (Fig.5 上)
・予想通り純音だが、倍音(640Hz)がわずかに見られる。100mm長の試験管を吹いたときの音(Fig.5 下)
・100mmの管の基音の波長はλ=4x0.100m=0.400m。振動数分析で実測した振動数はf=820Hz。音速はV=f x λ = 820 s-1x0.400m = 328 m/s。妥当な値である。・2倍音と3倍音のシグナルが僅かに見られるがほぼ純音である。
物理実験用の木製管楽器(Fig.6)
・ほぼ純音で、弱い3倍音が見られる。人の声 (fig. 7) 中学・高校生の声
・倍音の振動数を豊富に持っている。・楽器に比較して、個々の振動数の分布幅が広く、女子に比べて男子の声の分布幅が広い傾向にある。
4)議論
楽器による音色timbreの
違い、音高pitchについて次のような説明を時々見かける。
「楽器の音の高さは最も強度が大きい基音の振動数で決まり、基音の整数倍の振動数である倍音は強度は小さいが音に彩を添えて楽器に特有の音色を与える。」
この説明はわかりやすく一見本当そうに見えるが、「基音の強度が大きく倍音の強度は小さい」という説明が誤りであるのは今回の振動数分析からも明らかである。「音の高さ」について解きたい課題は次の2点:
1)
倍音のシリーズから成る音で最小の振動数である「基音」fundamentalが音を決めるのはなぜか?
2)基音を欠く倍音のシリーズ(missing fundamental)でも基音に相当する振動数が
音高となるのはなぜか?
これらは物理の問題なのか、それともヒトの知覚に関することか?
(A) 振動数と(B)周期の2つの観点から考えた。
楽器や人の声など「音高が明確な音」(ドラムなどは音高が明確でない)を、基音と倍音それぞれの振動数を持つ正弦波(純音)の集合として捉える。例えば、100, 200, 300, 400, 500 ・・・Hzの集合体。この場合、全ての純音に共通の周期を与える振動数は100Hzであり、これが「基音」として音高となる。つまり振動数の「最大公約数」が音高として聞こえる、とする考え方だ。Fig.8は、a=2π x100[Hz]として、200Hzなどの倍音全てが基音100Hzの周期を持つことを描いた。
「基音」の100Hzが欠けた集合(ミッシングファンダメンタル)、200, 300, 400, 500・・・Hzの場合も最大公約数は100Hzとなり、これが音高になると解釈できる。
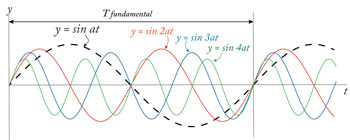 Fig.8 基音と倍音の正弦波のグラフ
Fig.8 基音と倍音の正弦波のグラフしかし、これは一種の法則としては理解できるが、なぜ最大公約数の振動数である基音が音高を決めるかは説明されていない。また、1600,1700, 1800, 1900, 2000Hzのような高い振動数の集合も最大公約数の振動数は100Hzだが本当に100Hzの音高だろうか?そうではないように思える。
(B) 正弦波を合成した波の周期
Fig.9は次のような正弦波と正弦波を足し合わせた波を描いたグラフである。
(a) 単純な正弦波。 基音のみの純音に対応する。
(b) 基音と2倍音〜8倍音までの正弦波を足し合わせたもの。青い破線で示したように「のこぎり波」と呼ばれる波形に近い形でその周期は基音の周期にほぼ一致する。
(c) 基音と奇数倍音、3倍音〜15倍音、の正弦波を足し合わせたもの。青い破線で示したように「矩形波」と呼ばれる波形に近い形でその周期は基音の周期にほぼ一致する。
(d) 上の(b)において基音の正弦波を除いた「ミッシングファンダメンタル」の音に相当する波のグラフである。(b)と同様に「のこぎり波」と呼ばれる波形に近い形で、その周期は基音の周期にほぼ一致する。
ヒトが「正弦波を合成した波の周期」で音高を認識すると解釈すると「音の高さに関する2つの課題」をうまく説明できるように思えるが、これは真実であろうか?また、前に述べた(1600,1700, 1800, 1900, 2000Hzのような)高い振動数の集合についてこの解釈との関係はどうなっているのだろうか?
(C) ヒトの音高認識
Fig.10はヒトの耳の構造4で、音波の振動は、鼓膜から3個の耳小骨に伝わった後、蝸牛(渦巻管)で電気信号に変換される。Fig.11は渦巻き状の蝸牛を模式化した図5で、蝸牛の内側に並んでいる有毛細胞がそれぞれ固有の振動数を認識する仕組を示している。
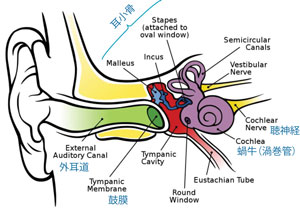 Fig.10 ヒトの耳の構造
Fig.10 ヒトの耳の構造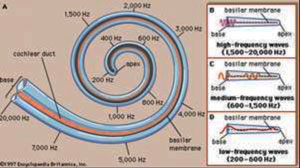 Fig.11 蝸牛(渦巻管)の構造
Fig.11 蝸牛(渦巻管)の構造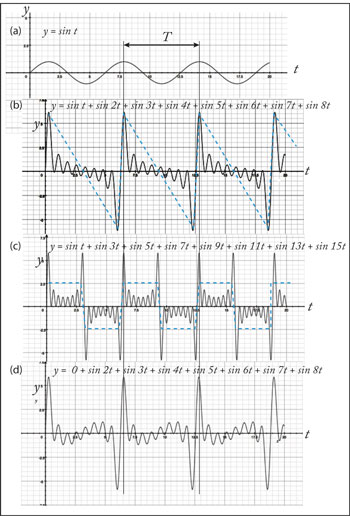 Fig.9 基音と倍音の正弦波を重ね合わせたグラフ
Fig.9 基音と倍音の正弦波を重ね合わせたグラフ多数の振動数を含む音(複合音)が耳に入ると、蝸牛はそれらの振動数を区別して認識する「生物的フーリエ変換分析機構」(文献2, p58)を持っている。しかし、蝸牛は音高そのものを決定するわけではなく、その分析結果を脳に送るだけである(文献2, p62)。多数の倍音を含む複合音の分析結果を蝸牛が電気信号で脳に送った後、脳がどのようにそれを基音の音高であると判断するかはよくわからないが、Fig.9からも推定できるように、「足し合わされた波の周期」が音高認識の主要因子であることは確かのようだ(文献2, p99)。
電気信号で音を作り出すシンセサイザーを考えてみよう。シンセサイザーが直接作り出す信号は振動数ではなく、周期を持ったいろいろな波形である。10 波形の基本的な形はFig.9のような、正弦波、のこぎり波、矩形波などである。波形は、楽器が発生するものを真似をして制作される。これらの波形を持った音がヒトの耳に入ると耳の中の蝸牛はそれを(フーリエ変換のように)振動数にわけてそれを電気信号として脳に送る。脳はこの信号からどのように「音高」を判断するのであろうか?こうして考えると現実の音の高さは明確な物理量で表せないことがわかる。
楽器の音高合わせ(チューニング)に用いる目的で、音高を測定するチューナーと呼ばれる機械がある。このうちクロマチック・チューナーは振動数の分布を測定して音高を決めているという。11 スマートフォンのアプリにPitchAnalyzerがあり、次の報告でこれを使用した。
(D)純音の複合による音の音高
倍音構造を持つ音の高さを脳がどのように判断しているかは、純音を足し合わせた「合成音」の音を作ればある程度推定できるのではないか?次の「11-14 音の高さとは(2)- 純音を合成した音の音高」でこれを実施した。
6)文献
1.H. E. White and D. H. White, "Physics and Music, The Science of Musical Sound" Dover Publications, Inc.(1980 original, 2014 Republication)音楽の物理に関する名著。400ページのほとんど全てのページにわかりやすい図を入れて解説している。
2.J. Schnupp, I. Nelken, and A. King, "Auditory Neuroscience、”MIT Press (2011).音を物理学と神経科学の両面から捉え、対応するインターネットサイトで実際に音を発生させて解説している。
3.Missing fundamental, Wikipedia.
4.Structure of the ear, uvex x-pertblog.
5.Cochlea duct, Britannica.
4.NHK高校講座、「第28回 音色ってなに?〜振動する弦〜
5.中川のビジュアル物理教室 音色
6.平野拓一、「音の周波数解析と楽器の音色について」(2003.2.26)
7.峯松信明, 「音響音声学」
8."Harmonics, Intervals, Instruments"
9.小林亮, 「音の波と三角関数』
10. シンセサイザー研究室
11. クロマチック・チューナー
教科書の記述