2つの音源の音の高さ(周波数)がわずかに異なるとき、「わーん、わーん、わーん・・・」のように強くなったり弱くなったりする「うなり」が発生する。うなりは、合奏において2個の楽器の音程が違うとき発生すると問題になる。パイプオルガンではトレモロ演奏に使われる。
1)実験 - 「うなり」の実演
Fig.1
使用器具: 低周波発信器(2台)、アンプ、スピーカー(2台)
ビデオでは次の条件を実施している。
100Hz + 105Hz
100Hz + 110Hz
1000Hz + 1010Hz
100Hz+105Hzの組み合わせでは、5秒間に25個のうなりを数えることができ、うなりの周波数が5Hzであることを耳で確かめられる。そのほかの組み合わせでは耳でうなりの回数を数えることは難しい。
2)イラストによる「うなり」の理解-1
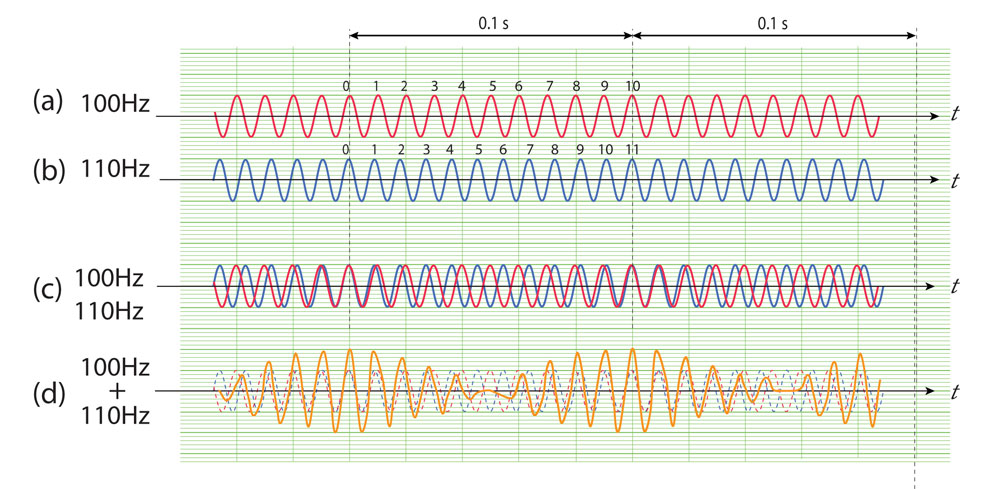
(c) 2個の波を重ねて描いた図。 (d) 2個の波が破線で描かれている。波に関する「重ね合わせの原理」、y = y1 + y2、で2個の波を重ね合わせたイラストが実線である。
この図で、重ね合わせた波は0.1秒の周期TBで強め合っていて、周波数fB=10Hzのうなりであることがわかる。
3)イラストによる「うなり」の理解-2
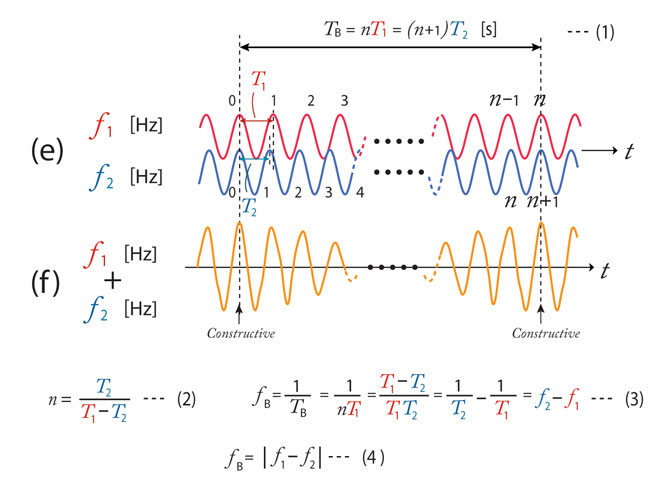
(e) 周波数 f1 の波1と周波数f2の波2の重ね合わせを考える。
ここでf1<f2、つまり波2の方が高い音であるとする。それぞれの音波の周期はT1=1/f1、T2=1/f2である。両方の波が強め合って(constructive)から次に強め合うまでの波1の山の数を
式(1)をnで解いて式(2)を得る。
うなりの周期fBは式(2)を用いてfB=f2-f1(式3)。
波1と波2の周波数の大小が入れ替わることを考慮すると 、うなりの周期fBは式(3)、つまり2個の音源の周波数の差となる。
3)音波の解析
使用器具:マイクロフォン(Vernier社LabPro(、インターフェース(Vernier社LabPro)、音波解析ソフトウェア(Vernier社LoggerPro)、PC(MacBook Air)
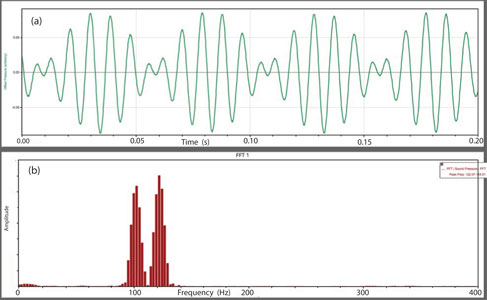
(a) 音の強度の時間変化の測定図 約0.15秒 の間に3回の繰り返しがあり、0.5Hzのうなりが生じていると読み取れる。
(b) 上の測定値をフーリエ変換した図で、横軸は周波数である。100Hzと120Hzに中心を持つ2個の音であることが示されている。
このように「うなり」は2個の音が干渉した結果生まれた強度の周期的な変化である。
4)うなりの数式表現
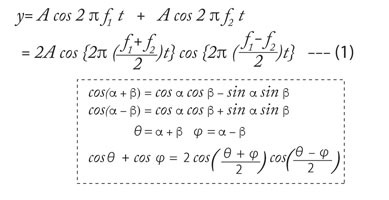
Fig.4
うなりを数学的に見てみよう。周波数 f1
[Hz] と周波数f2[Hz]で同じ大きさAの振幅を持つ2個の波を三角関数で足し合わせた式は、式(1)のように変形できる。式の変形は破線で囲んだ三角関数の公式を用いている。
式(1)で表される波は、(f1+f2)/2 [Hz]、つまり2個の波の平均の高さをの周波数を持つ波の振幅が(f1-f2)/2 [Hz]、つまり2個の波の周波数の差の1/2の周波数を持つ波で「変調」されていることを示している。「うなりの周波数」関係は下の数式のグラフの項で説明する。
5)数式のグラフと音声
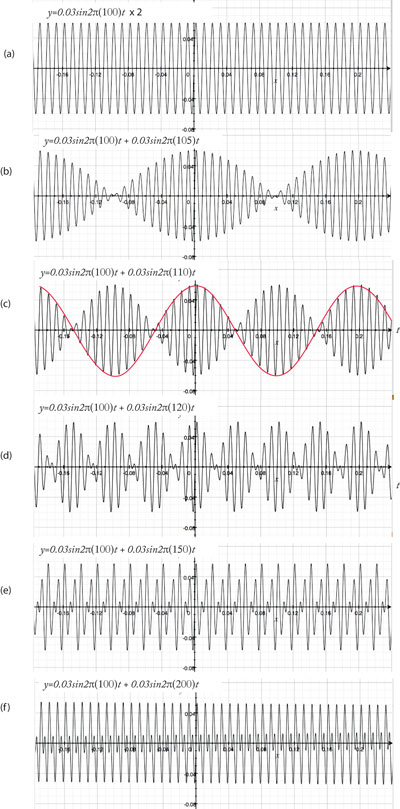
Fig.5 数式による音の正弦波の重ね合わせをグラフで表し、対応する音声を示した。
ソフトウェア:Apple "Grapher"(Mac OSX付属のグラフソフト)
NCH "Tone Generator", "WavePad"
(a)100Hz
(b)
100Hz +105Hz 20Hzの周期のうなりが発生している。
(c)100Hz +110Hz 10Hzの周期のうなりが派生している。2個の波の干渉の結果、105Hzの波が10Hzの周期で強弱を繰り返しておりこれがうなりの周波数である。一方、うなりの「波」は図の赤の実線で示したもので、その周期はうなりの周期の2倍であることがわかる。これが、
「うなりの数式表現」で現れた周波数、(f1-f2)/2 の意味である。
(d)100Hz + 120Hz 20Hzの周期のうなりが派生している。
(e)100Hz + 150Hz 2個の音の周波数が大きくなると、うなりとして知覚は難しくなる。この場合、50Hzの「差音」difference toneが知覚されるとも言われる。
(f)100Hz + 200Hz この組み合わせ(倍音)では2個の周波数の音があるにもかかわらず、単一の高さの音 100Hz として知覚されるのが興味深い。





